Pascal's Triangle

And Its Patterns

Pascal's Triangle was originally developed by the ancient Chinese, but Blaise Pascal was the first person to discover the importance of all of the patterns it contained. On this page, I explain how the Triangle is formed, and more importantly, many of its patterns.

How to Construct Pascal's Triangle
Sums of Rows	Prime Numbers	Hockey Stick
Magic 11's	Fibonacci Sequence	Triangular Numbers
Square Numbers	Points on a Circle	Connection to Sierpinski Fractal
hi	Polygonal Numbers	hi

How Pascal's Triangle is Constructed

At the tip of Pascal's Triangle is the number 1, which makes up the zeroth row. The first row (1 & 1) contains two 1's, both formed by adding the two numbers above them to the left and the right, in this case 1 and 0 (all numbers outside the Triangle are 0's). Do the same to create the 2nd row: 0+1=1; 1+1=2; 1+0=1. And the third: 0+1=1; 1+2=3; 2+1=3; 1+0=1. In this way, the rows of the triangle go on infinitly. A number in the triangle can also be found by nCr (n Choose r) where n is the number of the row and r is the element in that row. For example, in row 3, 1 is the zeroth element, 3 is element number 1, the next three is the 2nd element, and the last 1 is the 3rd element. The formula for nCr is:

n!
--------
r!(n-r)!

! means factorial, or the preceeding number multiplied by all the positive integers that are smaller than the number. 5! = 5 × 4 × 3 × 2 × 1 = 120.

The Sums of the Rows The sum of the numbers in any row is equal to 2 to the n^th power or 2ⁿ, when n is the number of the row. For example:

2⁰ = 1
2¹ = 1+1 = 2
2² = 1+2+1 = 4
2³ = 1+3+3+1 = 8
2⁴ = 1+4+6+4+1 = 16

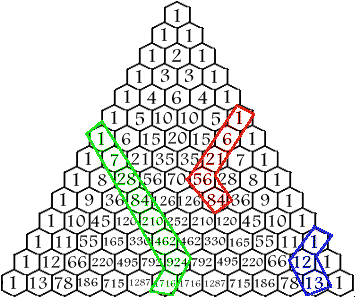
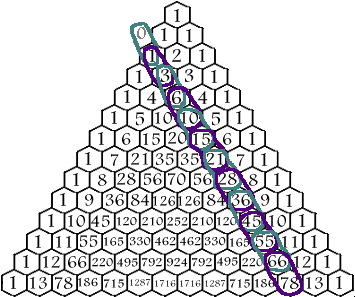
Prime Numbers If the 1^st element in a row is a prime number (remember, the 0th element of every row is 1), all the numbers in that row (excluding the 1's) are divisible by it. For example, in row 7 (1 7 21 35 35 21 7 1) 7, 21, and 35 are all divisible by 7.

Hockey Stick Pattern

If a diagonal of numbers of any length is selected starting at any of the 1's bordering the sides of the triangle and ending on any number inside the triangle on that diagonal, the sum of the numbers inside the selection is equal to the number below the end of the selection that is not on the same diagonal itself. If you don't understand that, look at the drawing.
1+6+21+56 = 84
1+7+28+84+210+462+924 = 1716
1+12 = 13

Magic 11's If a row is made into a single number by using each element as a digit of the number (carrying over when an element itself has more than one digit), the number is equal to 11 to the n^th power or 11ⁿ when n is the number of the row the multi-digit number was taken from.

Row #	Formula	=	Multi-Digit number	Actual Row
Row 0	11⁰	=	1	1
Row 1	11¹	=	11	1 1
Row 2	11²	=	121	1 2 1
Row 3	11³	=	1331	1 3 3 1
Row 4	11⁴	=	14641	1 4 6 4 1
Row 5	11⁵	=	161051	1 5 10 10 5 1
Row 6	11⁶	=	1771561	1 6 15 20 15 6 1
Row 7	11⁷	=	19487171	1 7 21 35 35 21 7 1
Row 8	11⁸	=	214358881	1 8 28 56 70 56 28 8 1

Fibonnacci's Sequence

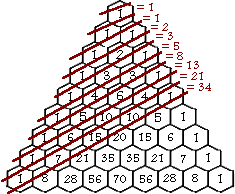
Fibonnacci's Sequence can also be located in Pascal's Triangle. The sum of the numbers in the consecutive rows shown in the diagram are the first numbers of the Fibonnacci Sequence. The Sequence can also be formed in a more direct way, very similar to the method used to form the Triangle, by adding two consecutive numbers in the sequence to produce the next number. The creates the sequence: 1,1,2,3,5,8,13,21,34, 55,89,144,233, etc . . . . The Fibonnacci Sequence can be found in the Golden Rectangle, the lengths of the segments of a pentagram, and in nature, and it decribes a curve which can be found in string instruments, such as the curve of a grand piano. The formula for the n^th number in the Fibonnacci Sequence is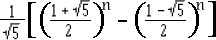

Try the formula out below (requires JavaScript)

Triangular Numbers

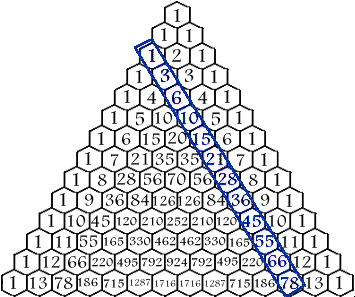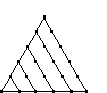
Triangular Numbers are just one type of polygonal numbers. See the section on Polygonal Numbers for an explaination of polygonal and triangular numbers. The triangular numbers can be found in the diagonal starting at row 3 as shown in the diagram. The first triangular number is 1, the second is 3, the third is 6, the fourth is 10, and so on.

Square Numbers

Square Numbers are another type of Polygonal Numbers They are found in the same diagonal as the triangular numbers. A Square Number is the sum of the two numbers in any circled area in the diagram. (The colors are different only to distinguish between the separate "rubber bands"). The n^th square number is equal to the n^th triangular number plus the (n-1)^th triangular number. (Remember, any number outside the triangle is 0). The interesting thing about these 4-sided polygonal numbers is that their name explains them perfectly. The very first square number is 0². The second is 1², the third is 2² (4), the fourth is 3² (9), and so on. Read on to the Polygonal Number section to learn more.

Polygonal Numbers Polygonal Numbers are really just the number of vertexes in a figure formed by a certain polygon. The first number in any group of polygonal numbers is always 1, or a point. The second number is equal to the number of vertexes of the polygon. For example, the second pentagonal number is 5, since pentagons have 5 vertexes (and sides). The third polygonal number is made by extending two of the sides of the polygon from the second polygonal number, completing the larger polygon, and placing vertexes and other points where necessary. The third polygonal number is found by adding all the vertexes and points in the resulting figure. (Look at the table below for a clearer explaination). My colleagues' formula (the Shi-Cheng formula) for the n^th x-gonal number (for example: the 2^nd 3-gonal, or triangular number) is:

If x is even, then:
y = x/2 - 1 and the formula is n+y(n²-n) If x is odd, then:
y = (x-1)/2 and the formula is (-(n²)+3n+2n²y-2ny)/2

These formulas work fine, but I think my own formula (the Winton formula) is much less convoluted, and is based on the fact that to find the n^th x-gonal number, you multiply the number in the 3^rd diagonal in the n^th row by x-2, and then add the number in that same row but in the 2^nd diagonal. Therefore:

((n²-n)/2) × (x-2) + n

Type	1^st	2^nd	3^rd	4^th	5^th	6^th	7^th
Triangular
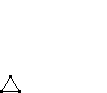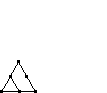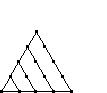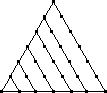Value	1	3	6	10	15	21	28
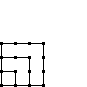
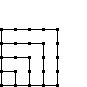
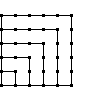
Square
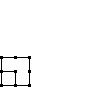Value	1	4	9	16	25	36	49
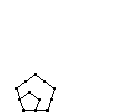
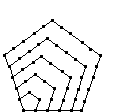
Pentagonal
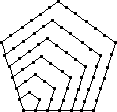Value	1	5	12	22	35	51	70
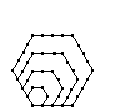
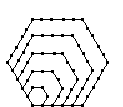
Hexagonal
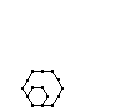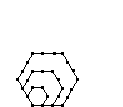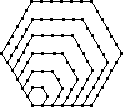Value	1	6	15	28	45	66	91

Points on a Circle

Image	Points	Segments	Triangles	Quadrilaterals	Pentagons	Hexagons	Heptagons
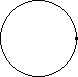	1
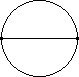	2	1
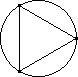	3	3	1
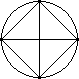	4	6	4	1
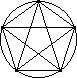	5	10	10	5	1
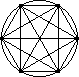	6	15	20	15	6	1
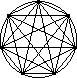	7	21	35	35	21	7	1

As you may have noticed, the numbers in the chart above are actually the tip of the right-angled form of Pascal's Triangle, except the preceeding 1's in each row are missing. The circular figures are formed by simply placing a number of points on a circle and then drawing all the possible lines between them. This chart shows that for a figure with n points, all you need to do is look at the n^th row of the Triangle in order to find the number of points, line segments, and polygons in the figure with ALL of their vertices on the circle.

Connection to Sierpinski's Triangle

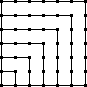
When all the odd numbers (numbers not divisible by 2) in Pascal's Triangle are filled in (black) and the rest (the evens) are left blank (white), the recursive Sierpinski Triangle fractal is revealed (see figure at near right), showing yet another pattern in Pascal's Triangle. Other interesting patterns are formed if the elements not divisible by other numbers are filled, especially those indivisible by prime numbers. Go here to download programs that calculate Pascal's Triangle and then use it to create patterns, such as the detailed, right-angle Sierpinski Triangle at the far right.

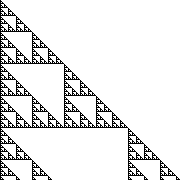Hit Counter